THE CIRCUITRY PATTERNS

We will examine the circuit diagrams of filters up to fourth-order, the most used in crossover circuits. Higher orders don't bring substantial benefits to listening, rather they introduce more than a few complications.

A first-order lowpass filter is simply formed by an inductor in series with the speaker. It produces a rolloff of 6dB/oct.:

Do you remember what we said about the behavior of capacitors in the fourth lesson? Well, replace the inductor with a capacitor and you'll get a first-order highpass filter with the same attenuation slope:

Now try to add a capacitor to a first-order lowpass, but in parallel with the speaker this time. The capacitor — which is totally transparent to the highs — actually diverts them toward ground, helping the inductor to reject unwanted frequencies with better effectiveness. This way you'll have gotten a second-order lowpass filter, with a characteristic rolloff of 12dB/oct.:

Now start from a first-order highpass filter and reverse the above statements. There, the second-order highpass you asked for:

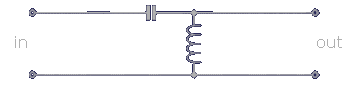
Schematically you can think of a third-order lowpass filter as a second-order one with the addition of a second inductor in series. Its characteristic rolloff is equal to 18dB/oct.:

Inversely, the third-order highpass will be formed by a capacitor in series, an inductor in parallel, plus a second capacitor in series:

The rolloff of a fourth-order lowpass is equal to 24dB/oct. It is formed by an inductor in series, a capacitor in parallel, plus a second inductor in series and a second capacitor in parallel. Surely the most attentive of you will realize it is similar to two second-order lowpass cascading filters:

The list is one short without the fourth-order highpass, but at this point of the story you should be able to guess what it is by yourself:

Who's not clever enough to solve the problem is strongly suggested to take a deep breath and start all over again. In the meantime we'll be drawing the numbers