L'IMPEDENZA DELL'ALTOPARLANTE

In questo paragrafo cercheremo di demolire il mito secondo cui l'impedenza di un altoparlante corrisponderebbe a quella dichiarata dal costruttore. Diciamocelo subito, credere a corbellerie come questa equivale a credere che i bambini li porta la cicogna.

In realtà l'impedenza nominale, quella specificata sui cataloghi, ha il solo scopo di suddividere gli altoparlanti per famiglie, in funzione del tipo di utilizzo cui sono destinati. Avremo così altoparlanti da 4Ω per il car-audio, da 8Ω per l'hi-fi domestica e da 16Ω o più per applicazioni professionali. Il dato nominale dovrebbe approssimare al più vicino di questi valori l'impedenza reale misurata sulla bobina mobile a certe frequenze — tipicamente 100hz, 400hz, 1Khz, ma non solo, secondo il costruttore e il tipo di altoparlante. Essendo il dato nominale riferito ad una sola frequenza, per di più in modo approssimato, ed essendo invece l'impedenza variabile in funzione della frequenza, è di tutta evidenza che non potremo far riferimento a questo valore per il calcolo del filtro. Se poi aggiungiamo che non è raro imbattersi in costruttori che spacciano per componenti da 4Ω altoparlanti di impedenza anche doppia, allora il quadro è completo.

È possibile descrivere l'impedenza assunta dalla bobina mobile alle varie frequenze in forma grafica su un piano cartesiano, con in ascissa la scala delle frequenze (Hz) e in ordinata i valori di impedenza (Ω). Il disegno che ne deriva è chiamato curva di impedenza e rappresenta visivamente la modificazione del valore ohmico assunto dall'impedenza alle diverse frequenze. Ecco ad esempio quello di un midrange a cono dichiarato per 6Ω nominali:

La prima cosa che notiamo è un picco di impedenza con un fronte di salita e un fronte di discesa speculari fra loro. Ad esso corrisponde la frequenza di risonanza del componente, riconoscibile appunto perché alla risonanza tutti i trasduttori mostrano un repentino innalzamento dell'impedenza. (Si noti come la specularità della campana sia verificabile solo ove la scala delle frequenze in ascissa sia logaritmica). Spostandoci verso destra, ossia salendo con la frequenza, incontriamo una zona a sella entro cui dovrebbe essere possibile riscontrare un valore prossimo a quello dichiarato come nominale — vale quanto detto prima su alcuni costruttori — dopodiché gli effetti dell'induttanza della bobina mobile cominciano a farsi sentire, in forma di un graduale aumento dell'impedenza misurabile.

Dai due grafici qui sotto potete rendervi conto di come un generico filtro passa-banda del II ordine, calcolato con le formule che Vi abbiamo fornito produca risposte totalmente differenti se chiuso su un resistore (verde) o su un generico midrange (giallo):

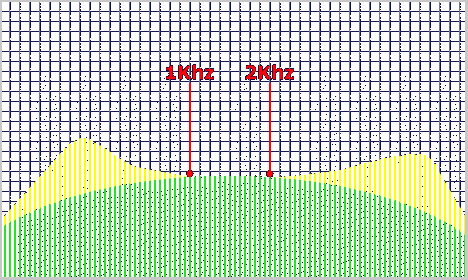
Sia alla risonanza del midrange (attenzione! non si tratta dello stesso trasduttore dell'esempio precedente) che alle frequenze più alte, il filtro vede un'impedenza di carico maggiore e filtra meno. Risultato: le due curve sono uguali solo nell'ottava 1Khz-2Khz e le porzioni di frequenza che il filtraggio doveva reiettare sono invece prepotentemente in evidenza. Bella schifezza!

Per trovare corrispondenza fra la risposta del complesso filtro/altoparlante e il modello teorizzato dalle formule è assolutamente necessario modificare l'altoparlante affinché esso presenti ai suoi morsetti un'impedenza il più possibile resistiva, cioè costante con la frequenza. Assolvono proprio questa funzione le reti di equalizzazione